Previous posts in this series on MCMC samplers for Bayesian inference (in order of publication):
- Bayesian Simple Linear Regression with Gibbs Sampling in R
- Blocked Gibbs Sampling in R for Bayesian Multiple Linear Regression
- Metropolis-in-Gibbs Sampling and Runtime Analysis with Profviz
The code for all of these posts can be found in my BayesianTutorials GitHub Repo.
In the most recent post, I profiled a Metropolis-in-Gibbs sampler for estimating the parameters of a Bayesian logistic regression model.
The conclusion was that evaluation of the log-posterior was a significant run time bottleneck. In each iteration, the log-posterior is evaluated twice: once at the current draw, and another at the proposed draw.
This post hones in on this issue to show how Rcpp can help get past this bottleneck. For this particular post, my code and results are in this sub-repo. If you’re short on time, TLDR: just by coding the log-posterior in C++ instead of a vectorized R function, we can significantly reduce run time. The R implementation runs about 4-7 times slower. If you’re coding your own samplers, profiling your code and re-writing bottlenecks in Rcpp can be hugely beneficial.
I simulate data from a similar model as in the previous post:
For this analysis I coded two Metropolis-Hastings (MH) samplers: sample_mh() and sample_mh_cpp(). The former uses a log-posterior coded as a vectorized R function. The latter uses a log-posterior coded in C++ (log_post.cpp) and compiled into an R function with Rcpp. The Armadillo library was useful for matrix and vector classes in C++.
So let’s see how the sampler using C++ does. I ran 100,000 MH iterations with a jumping distribution covariance of , where
is the
identity matrix. So in each iteration, a vector of coefficients is proposed. In this sense, the sampler is a “blocked” MH. The chains are plotted below with red lines indicating parameter values under which the data were generated.

The chains seem to converge. The average acceptance probability converges to about 20% over the sampling run.
Side note: in this case, where is 4-dimensional, MH works well. But it’s well-known that in higher dimensions, MH does not work so well (it explores the posterior slowly). In that setting, adaptive MH works a little better and Hamiltonian Monte Carlo (HMC) probably works the best.
Adaptive MH includes a tuning period where we update the variance of the proposal distribution – scaling the proposal variance appropriately depending on if the acceptance probability is too high or too low.
HMC uses an additional “momentum” variable to make the exploration of the posterior more efficient. I’ll probably discuss these in future posts.
So how does the Rcpp implementation compare to the R implementation? The run time is significantly lower for Rcpp. When the log-posterior is coded as a vectorized R function, the sampler runs about 7 times slower relative to the Rcpp implementation (for sample size of 100). The plot below shows relative run time for sample sizes of 100 to 5000 in increments of 500.
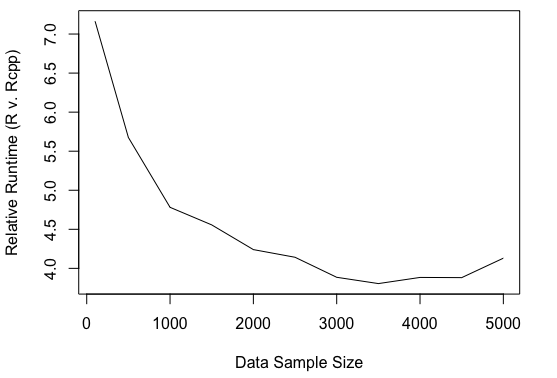
I’m not so sure exactly how to interpret this leveling out of relative run time as sample size increases. It seems to level out to a relative run time of about 4.
Intuitively, there is some fixed efficiency gain that C++ brings. It’s probably worth looking into this more and understanding exactly where the efficiency gains are coming from and why it levels out. But it’s clear that Rcpp is a good solution to bottlenecks in your code. This is worth doing especially if you’re developing new Bayesian methods that require custom samplers.
2 thoughts on “Speeding up Metropolis-Hastings with Rcpp”